[Sailor Steve]

Originally Posted by Nemo66

uff..Steve...proof? Nope, not at this very moment, Sir

I definitely remember that i read about this, especially about the handiness of the Type VII in comparison to the allied destroyers, in several german historical naval books.

Fair enough. I was just curious to find out what others have said on the subject.

And what do you mean with "tighter"? Does this mean as smaller circle? (Sorry, i am german)

Yes and no. The circle is tighter at slower speeds, but the ship travelling at a higher speed goes around the circle faster.

In my understanding the turning circle gets smaller/tighter when a ship goes slower, and the turning circle is a bigger/wider one when it goes faster, because of the centrifugal forces. This way it is modelled in SH3 too. But you can't really notice that fact in open seas because you have no relation points.

Here is what they observed with HMS Dreadnought on her trials in October 1906. At 12 knots Dreadnought had a Tactical Diameter of 442 yards. At 20 knots her TD was a slightly wider 466 yards.

The problem is that at 12 knots it took her 50 seconds to turn the first 4 points (45 degrees) and 85 seconds to turn the first 8 points (90 degrees).
At 20 knots it only took 40 seconds to turn the first 4 points and 61 seconds to turn the first 8 points. This means that while the turning circle was wider at the higher speed the ship actually got turned around faster.

One of the things not mentioned in that account is that if Dreadnought turned her first 4 points in 40 seconds and her first 8 points in 61 seconds, that means that she turned her second 4 points (45 to 90 degrees) in only 21 seconds. Taken altogether this means that once she was fully into the circle that big fat battleship was turning 135 degrees every minute, which is much faster than any game (tabletop game anyway) gives her credit for. Of course she would also be slowing down dramatically at the same time, and would keep doing so until she reached a balance between acceleration and speed loss, which in this case seems to be that previously mentioned 12 knots.

If you try this in narrow waters (small bay f.e.) you will see what i mean instantly. This seems perfectly logical to me, the centrifugal forces push the ship outwards, out of the curve, so a faster ship creates more centrifugal forces and therefore will need more space to turn.

That is true of cars and airplanes, and boats to some degree. Ships, however, have what is called a 'Displacement Hull', which means that while the ship will heel outward at higher speeds the actual hydrodynamic effect is to push the ship inward, not outward. Give the ship right rudder. The stern is pushed to the left. The water on the left side forces the bow to turn right. As the pressure on the left side (outside of the circle) builds up the bow is forced to turn tighter.

'Tactical Diameter' is the measure of the first 180 degrees the ship turns, after which it settles into the actual circle it will be travelling. Here are a couple of good charts explaining how it looks.





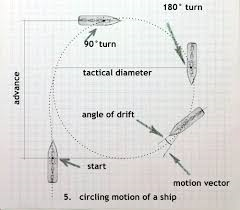
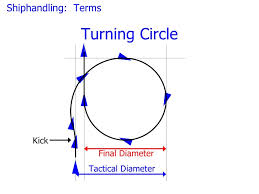
It is also true that a ship travelling at a very slow speed (1 or 2 knots) is almost unmaneuverable. The bigger the ship the worse this becomes.

Also a shorter ship should do a smaller turn with less need for space than a longer one. As the type VII subs were about two thirds the length of a Destroyer i think this is an argument, too.

That's true, if the ships are travelling the same speed. A submerged U-boat travelling at 2 knots will take a very long time to turn at all, and its circle will be quite wide. At 8 knots it will turn much faster and the circle will be tighter (smaller). The destroyer at 12 knots will certainly have a wider circle but it will turn that circle much more quickly.

This is probably part of the reason that smaller escorts like the corvettes were so effective. They were shorter than the U-boats and had smaller turning circles, but at 12 knots they could still turn tighter than the slower submarine.

Anyway, i read about it in different books by different authors, some of them Ex-Kriegsmarine Kaleuns so i think i can be pretty sure about it. But proof..? Sorry, not at this very moment, sir

That's cool. I'm not demanding immediate proof. If you have the books then I'm sure it's there.

P.S.: Maybe it's just a misunderstanding. I am talking about how narrow/small a turning circle can be. And i think you relate to the speed/time a ship could finish a full circle. Can this be the case? For example the Richthofens Fokker Triplane in WW1 was kind of slow, but very handy, that means it could do a more narrow turn/curve. Just like the sub. The DC must go a longer way to finsih its circle than the sub does. Just imagine two circles, one being signifantly smaller. After the first waterbomb attack, the Dc has to do a bigger/wider circle than the sub, no matter if he is faster. That's exactly what i am referring to.

Yeah, I think you're right. In fact the airplane comparison is a good one. Pilots of planes like the Fokker D.VII and SE.5a had to learn new tactics to take advantage of their speed and had to learn not to dogfight with planes like the DR.I and Camel. The same was true for Allied pilots in the Pacific in WW2. The destroyer has to pull away from the U-boat and then turn back and try again. And again, this is why the corvette has the advantage.

Information above from The Battleship Dreadnought, by John Roberts, Conway Maritime Press, London, 1992