[TorpX]

It is commonly believed that cruising around at good speed is essential to searching on patrol. It seems to have become accepted wisdom, that this not only produces better chances for finding a contact, but that the odds are dramatically improved by doing so.

Since this topic comes up periodically, I decided to try to figure out a proper solution to the question of how much continuous cruising helps ones chances of finding a contact.

First off, we need to make some general assumptions about the conditions. I am going to assume that we know the direction of the prevailing shipping traffic, and that the odds of a target transiting through any portion of our search area is the same as for any other area of equal size. That is, that shipping is equally distributed (which it would be, at least as far as we know). I consider it fairly obvious that the best "search pattern" is one that cuts across the greatest number of potential target routes in a given length of time; that is, moving perpendicular to traffic. This means that fancy box or 'x' patterns are less effective, and moving parallel to the direction of traffic is just a waste of fuel.

In the diagram below, we have our sub moving east to west, and enemy traffic moving north to south. We could change the directions any number of ways; the important thing is that our sub is moving perpendicular to shipping traffic. The black lines at either side is the search limits we have marked off for our sub. It will go east to west until it reaches the west limit, then reverse course and go east until it reaches the east limit, and so on. The gray circle is the sub's detection bubble. Any target that comes within that space will be detected. The red arrows represent potential target ships. At first blush, we might be tempted to think that all, or most, of these targets would be detected, but this isn't the case. If we were to stay in place, we would expect to find #6 and #7. Moving to the west, we might hope to find #1 to #7, but it is possible, even likely, that #1, #2 and #3 would get by before we get far enough west, and #7 and the rest would be safe because we will be over to the west as they go by. So the question is how many targets are we likely to detect, compared to the same situation, where we are sitting still?

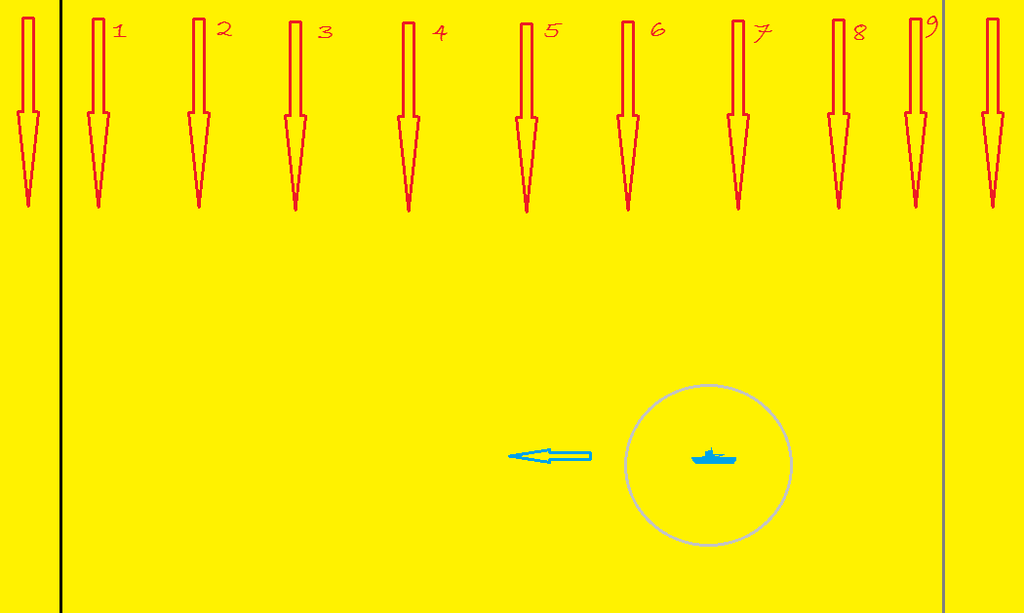
We might try to plot out the route and timing of every potential target, dividing the sea lane into 1 nm strips, but life is short and there must be a better way to go about this.

If we adopt a different frame of reference, the problem is soluble. Below, I have diagramed the movement of our sub, using an enemy ship as a frame of reference, instead of a fixed earth frame. The sub appears to move in a zig-zag pattern, though it is really still going east-west. The sub is starting at point A moving to B, reversing course until C, and going east once more to D. At D the sub is again in the middle of it's search zone and the cycle will repeat. I'll explain the reason this is important later. Essentially, we have used vector addition to subtract the target speed, from both sub and targets.

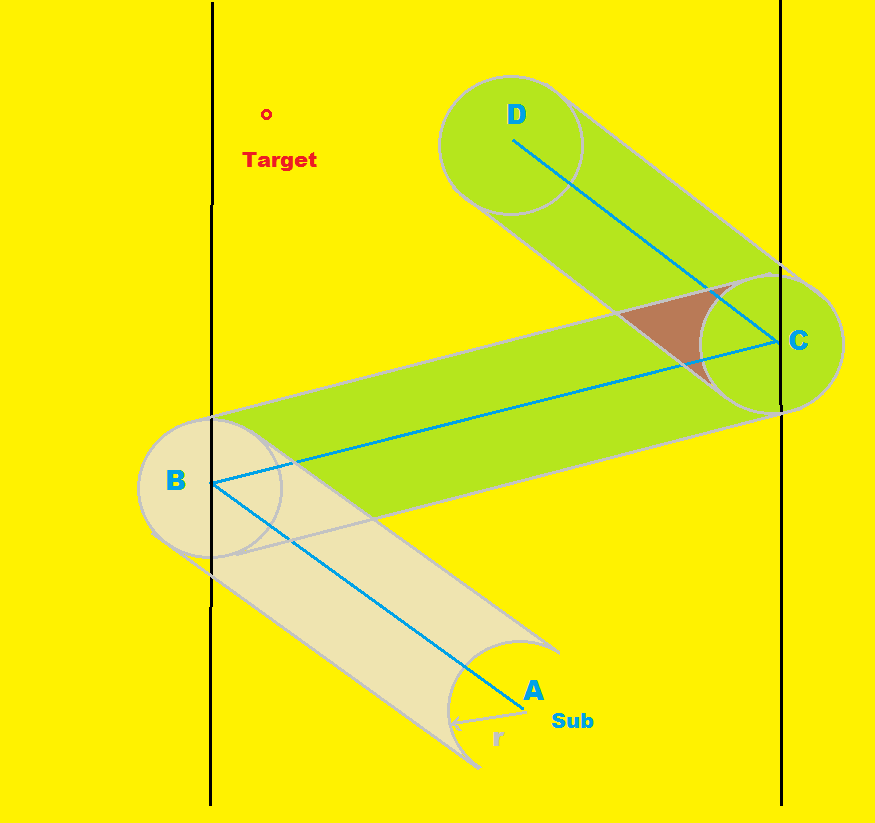
Note that, using this frame of reference, the target ships do not move. Any target that falls within the searched area, will be located, any that are outside will not be. I call the areas computed in this frame, pseudo-areas. I shaded the first segment, AB, manila so we can see that it is a rectangular segment, with a missing semi-circle at one end, and a extra semi-circle at the other. The remaining segments are light green. The concave area at A is there because we only want the newly searched area after the sub passes A. Since this geometrically is equivalent to the semi-circle past B, we can see that the area of this segment is equal to the length of A to B times the width of the segment (2r). Also, it is easy to conclude that the segment CD is the same length as AB and the segment BC is twice AB. So if we multiply the area of segment AB by 4 we should have our total pseudo-area searched by our moving sub.

But wait a minute; there are parts of this area that would be counted twice if we do that. See the wedge shaped area in brown (near C). There is also an equivalent area near B. For accurate results, we mush subtract the areas there, lest we overestimate our search ability. This stems from the fact that when we reverse course, we will be searching an area that we already searched minutes before, so we have to expect some loss of efficiency there. This is why we must be careful to have the sub move a complete cycle; otherwise, we could not properly account for the overlapping sections.

To obtain a ratio for the probability of finding a contact by a moving sub relative to that by a stationary sub, we need to know r, the detection radius of our sub, w, the distance from the center of the search zone to either edge, and b. b is the angle between the horizontal and the line AB. The angle ABC is 2b, as is angle BCD. It depends on the relative speeds of the target and sub.

So, we seek to compute 3 quantities:

1. the roving 'pseudo-area' (i.e. the area of the 3 segments we diagramed).
2. the 'wedge-shaped pseudo-area' (to account for the overlapping).
3. the comparable 'pseudo-area' for a stationary sub.

Note that, for a stationary sub, the graphical representation would be one large segment of the same width, 2r, going from A to D.

For number 1. we have:

Roving 'pseudo-area' = 8*r*w / cos b

where

r is the detection radius of the sub
w is the width of the search zone from the center to one edge (i.e. half of the full width)
b is the angle Arctan (Vt / Vu)
Vt is the target speed
Vu is the sub speed


For 2, the 'wedge area', we have:

[I won't go into the details of finding this. Extra credit for those who can figure this out. Note that the faster the sub goes back and forth, the greater the overlap there will be. For typical values, it shouldn't be too large.]

'wedge pseudo-area' = 2r^2 * [tan(90-b) - pi*(90-b)/180]

For the static sub computation we can calculate the time interval for the moving sub to complete one cycle, and then substitute that value in the equation for the area, to get our final result.

The time t = 4w / Vu, and the pseudo area = 2r * t * Vt.

This gives us:

Stationary 'pseudo-area' = 8*r*w * (Vt/Vu)

For a concrete example, I will use a value of 20 nm for w, 10 nm for r (this is the max. rendering distance for SH4), a Vt of 8 kn. and a Vu of 9 kn.

These values give us 41.63 degrees for b.

The Base 'pseudo-area' is 2140.7.

The 'wedge psuedo area' is 56.2.

The Stationary 'pseudo-area' is 1422.2.

Efficiency Ratio = (Roving PA - Wedge PA) / Stationary PA

So, for these numbers we have a ratio of 1.466.


In other words we can expect to obtain 46.7% more contacts under these circumstances.


How valuable is a 46% 'search bonus' for a moving sub? Well, a lot depends on how much fuel we have to play with. If we have plenty to spare, there would be little reason not to use some for roving. If, on the other hand, our supply is tight, and roving would mean cutting our patrol time in half, it isn't very good at all.



Tomorrow, I will post results for various sub and ship speeds, and add a few thoughts.

-TorpX