Alright, some theory crafting regarding hydrophone range and bearing accuracy based on different sources. Thank you, gap, for pointing me to them.
[1]
http://www.cdvandt.org/GHG1996.pdf
[2]
http://de.wikipedia.org/wiki/Gruppenhorchger%C3%A4t
[3]
http://www.sengpielaudio.com/calculator-spl.htm
[4]
http://www.sengpielaudio.com/calculator-levelchange.htm
[5]
http://www.forum-marinearchiv.de/smf...?topic=4469.15
The following calculations are based on very little data and lots of assumptions and last but not least, I'm not sure whether I have applied the maths involved correctly.
I'll assume a GHG (group listening apparatus) hydrophone and a merchant at 12-13 knots as target contact, since [1] provides some data on this scenario, and this is a common encounter in sh5.
First: max range under optimal conditions, that is:
- no noise
- contact on a relative bearing of 90 degrees starport or 270 degrees port
[1] says: 20 to 25 nautical miles, that is 37km to 46.3km for single contacts
[2] says: 20km for single contacts
I'll go with something in the middle, which, as far as i know, happens to be the max range the game starts to make contact pickups by hydrophone possible:
At R = 30km under optimal conditions, we can barely hear the contact.
At 90 (or 270) degrees the sound hits the hydrophones perpendicularily, i.e. the full sound pressure stimulates the hydrohpone membranes. If we deviate from that bearing, the sound waves come in aslant, and only a portion of the sound pressure is effective on the hydrophone. That portion is proportional to the cosine of the deviation from 90/270 degrees:
maxrange = R * cos(alpha), with alpha = deviation from 90/270 degrees
On to bearing accuracy: The GHG features 4 settings for the high pass filter[1]:
- off: no filtering, complete received sound usable, bearing accuracy 8 degrees (I understand this as +-4 degrees)
- 1kHz: frequencies below 1kHz are filtered out, uses frequencies from 1kHz - 7kHz, yields a bearing accuracy of 4 degrees
- 3Khz: frequencies from 3-7kHz used, yields a bearing accuracy of 1.5 degrees
- 6kHz: frequencies from 6-7kHz used, yields a bearing accuracy of < 1 degree
The maxrange depending on bearing, that we calulated above, applies to the "off" setting. As soon as we start filtering frequencies to achieve better bearing accuracy, the sound gets softer and we need to be closer to the contact, so we can still hear it. But how much closer?
[1] says: the merchant at 12-13 knots produces a maximum sonic spectrum at 100Hz, and only 10% at 4Khz, which we can hear using the 3Khz setting. Fortunately, filtering out 90% of a sound does not mean, that the sound pressure usable at the hydrophone drops by 90%. [3] has some explanations and calculators about this topic. I assume, the sounds at different frequencies produced by the engines are equally loud. If we add up 10 equally loud sound sources with different fequencies, the sound level increases by 10dB. Conversely, the sound level of those 10% at 4kHz is 10dB less than the sound level of the whole, unfiltered sound. This level change is called "Delta L". The formula is not quite as simple as it looks like from this particular example (see [3], Adding levels of equal loud sound sources).
What does a 10dB decrease of the sound level mean regarding the usable sound pressure at the hydrophones? According to [4], the sound pressure factor y = 10^(Delta L / 20): For -10dB, this is around 0.316.
Sound pressure is reciprocally proportinal to distance.
So, at a bearing of 90 degrees, under optimal conditions, we can barely hear our contact at 30km and determine its bearing +-4 degrees. If we wanted to use the 3KHz setting and determine its bearing +-0.75 degrees, we need to be closer than 30km * 0.316 = 9.48km.
Time for some more assumptions regarding the other hydrophone high pass filter settings, that are not covered by [1]:
Given that 10% are above 4kHz, let's assume 33% (i.e. one third) of the sound emissions of a merchant at 12-13 knots are above 1Khz, and 3% (i.e. 1/33rd) are above 6kHz.
This leads to the following sound pressure factors:
Code:
cutoff-frequency None 1kHz 3kHz 6kHz
Portion of the sound 100% 33% 10% 3%
Decrease of sound level 0dB -4.77dB -10dB -15.18dB
Sound pressure factor 1 0.577 0.316 0.174
bearing accuracy +-4 +-2 +-0.75 +-0.5
Let's combine the two results (reduced maxrange depending on the bearing as well as on the selected high pass filter) and visualize them.
We have four functions, one for each high pass filter setting. The x-axis is the bearing deviation from 90/270 degrees. The y-axis shows the maximum range in km at which we can hear the contact using a specific high pass filter setting.
Code:
Blue(off) : f(alpha) = 30km * 1 * cos(alpha)
Red(1kHz) : f(alpha) = 30km * 0.577 * cos(alpha)
Green(3kHz): f(alpha) = 30km * 0.316 * cos(alpha)
Gray(6kHz) : f(alpha) = 30km * 0.174 * cos(alpha)
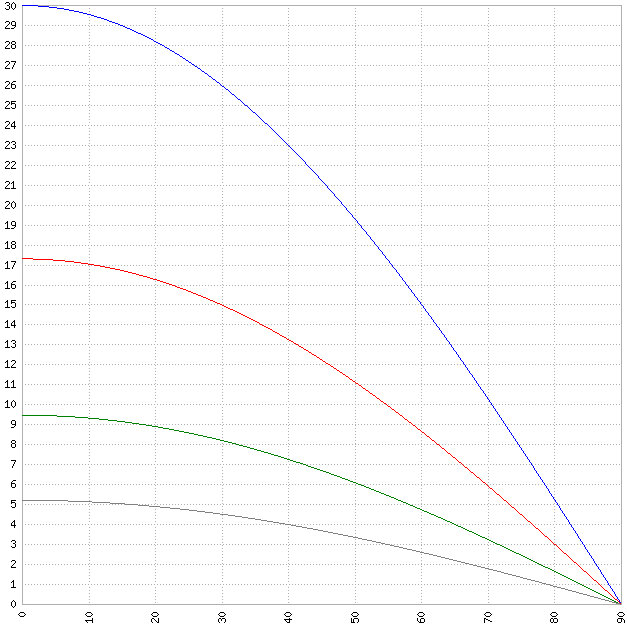
These results correspond to [5], which (I think) cites from E.Rössler, Die Sonaranlagen der deutschen U-Boote. In a GHG-Test performed in February 1943, the type IX sub U-194 was not able to detect a contact in a distance of 4km on a bearing between 348 and 10 degrees. This test report also has some data on the GHG range while the sub is moving at different speeds.
Feedback is very welcome. Maybe I should have used sound intensity instead of sound pressure? Maybe assumptions are just plain wrong? Otherwise I'm planning to base the mod on this model.