[Svonne]

Step four:

Using the compas, draw a circle centered at the end of the measurement you just did (labeled P3b in the image). The radius of this circle should be your intercept speed. In this example, I think I have a good angle of aproach, and don't feel like wasting too much fuel, so I leave the circle's radius at 12kms, representing the 12 knots to wich I'll speed up to to intercept the target. Take special notice of where the circle intercepts the leg of the protractor that goes from your ship to the contact (labeled P1b in the image). Your nav-map should look like this:



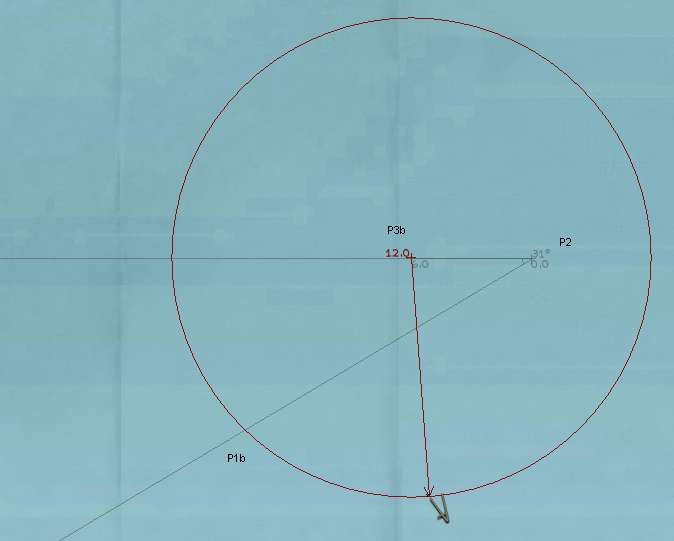Two points of interest here. First; you can choose whatever intercept speed that you desire (within reason). If the contact is coming somewhat towards you, and isn't too far away to begin with, you can intercept very easily with an economical 9knots speed for your U-boat. If the contact is heading away from you, or is too far, or is moving very quickly, you will most likely want to use a quicker speed, but never, ever use flank speed... it's just a waste of fuel when used in long range maneuvers like this. The second point of interest is the use of the circle to measure your U-boat's speed instead of a ruler. The reason for this is simple: you're supoused to measure this distance along the course that you will take to intercept the contact... but how can you do that if we haven't figured out yet what that course will be?... luckily the circle's radius measures distances IN EVERY DIRECTION (all around) and that's why we use it.

Also, rember to be consistent in your scale choice, by using the same scale as the one you used to measure the contact's speed. If your drawn circle is so small that it does'nt make a P1b point in your diagram (i.e.: it does'nt touch the line between your U-boat and the contact) then that means that the intercept speed you have chosen is too slow, and you'll never be able to catch the contact. Chose a faster speed thus making a bigger circle. Also, on very rare ocations, when the contact's speed is superior to your's (but an intercept is still possible), the circle might touch the U-boat/contact line in TWO places. In that case, the point of interes (P1b) is the the closest one to your U-boat.

Step 5:

With another protractor tool, click at the center of the circle (P3b), then the point where the circle intercects the line that goes from your U-boat to the contact (P1b), and from there click in the direction of the contact. TAKE NOTICE OF THIS IMPORTANT ANGLE... Lets call it Angle A. Your nav-map should look like this:



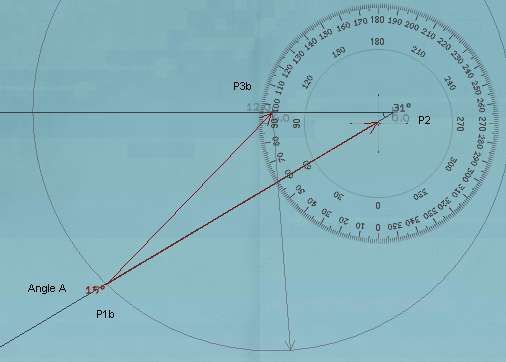The easiest way to do the last leg of this protractor would have been to actually click on the contact for the third (last) click. However, this is not really needed... al we care about is the angle that is being formed and that will remain the same if you click exactly on the contact or in any other point that is in the same exact direction.

Step 6:

Using yet another protractor tool, click on the vicinity of the contact (if you can't click exactly on the contact because of all the overlaping protactors, then simply click somwhere along the line formed by your U-boat and the contact), then on your u-boat, and then drag the second leg of the protractor so that it PERFECTLY REPLICATES ANGLE A. That's it, your done: Point Three, indicated by the thick black arrow in the image below is where the target is going to be just at the moment of interception... SO START HEADING FOR IT, HER KALEUN!!!



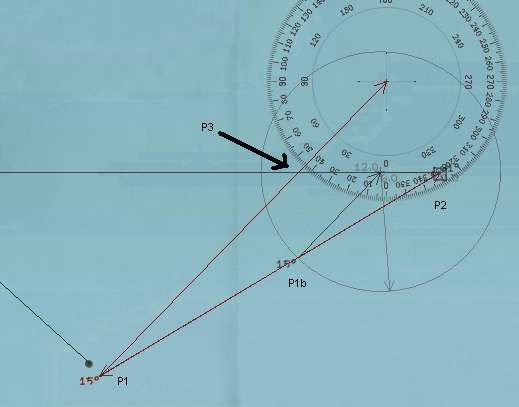Here's the magic of trigonometry at work. The little triangle you made in figure 5 (points P1b, P2 and P3b) solves the problem of interpecting the target IF your U-boat where positioned perfectly for a one hour interception course (it would have to start at P1b). Our situation isn't as ideal of course, but pitagoras says that what holds true for little triangle holds true for big ones, as long as all their inner angles are the same. So, if your intercept took two hours instead of the one hour represented by the small triangle, your solution triangle would be bigger by a factor of two, and your U-boat would have to start at a point twice as far away from the contact as point P1b, but you'd still have the SAME INNER ANGLES in your solution triangle as in the little one. In our case it will take X amount of hours (unknown as of yet) to intercept, so our solution triangle would be bigger by a factor of X (which we don't know) and our U-boat would have to start from our present location (which is great for us) and our solution triangle would still have the all the same inner angles (which we DO know) as the little one... that's why we replicate angle A with our last protractor.

Keep in mind that the result may not allways be so perfect that you end up ramming the enemy ship. Theoreticaly it should, but there are several limiting factors to this method:

1)Being a grafical solution, it depends greatly on your ability to draw correctly and exactly, with very high precision. Each mistake done with the drawings whill lead you to a less than perfect result (use high zoom-ins on the nav-map to mimize this potential for error)

2)The data provided to you was vage and imprecise in nature (the targets speed and heading)

3)Enemy ships don't travel in a straight line forever, so you have to intercept them before they make any significant course changes, otherwise you'll miss them.