[TorpX]

I've put together a few examples so people can look at some specific numbers, and check the math if they so desire.

Ex. A1
track angle : -120
gyro angle : 40
sub speed : 2
target speed : 6
target range : 1200
target bearing: 55 deg.

torpedo config:
torpedo speed: 20
q : 120 'torpedo reach
r : 100 'turning radius
Lg : 4 'launch lag
bb : 30 'bow tube distance

Note that all figures are in coherent units; i.e. ranges in meters, times in seconds, and speeds in meters per second. This makes checking the math much easier. Of course, in the finished program, speeds will be in knots.

start readout
Kd 0.26146582 'sub functions
Kx 18.0519046
Ky 12.3208889
Kz -118.17693
Px 222.278761
Py 23.3955557
TT 1 'torpedo tube status, 1= bow, -1= stern

t1 22.1297521 'time intervals
t2 13.4906585
t3 42.90395

T0x 688.291724 'x and y coordinates of sub, target, and torpedo
T0y 982.982453
T1x 754.68098
T1y 867.992888
T2x 795.152955
T2y 797.89337
T3x 923.864805
T3y 574.957907
U1x 44.2595041
U1y 0
U2x 71.2408212
U2y 0
U3x 157.048721
U3y 0
P2x 266.538265
P2y 23.3955557
P3x 923.864915
P3y 574.958105

tgt bearing at launch: 50.7008883
tgt bearing at impact: 36.8625251

Torp Track 1047.89217
Error: 0.22621151e-3 'error between computed torp and target positions
Ath1: 5.23598776 'relative target heading, radians
in deg.: 300
Abg1: 0.95993109 'relative target bearing, radians
in deg.: 55
Agyo1: 0.6981317 'gyro angle, order, radians
in deg.: 40

At t = 0
target is at T0
sub is at U0
sub computes firing solution

At t = t1
target is at T1
sub is at U1
sub launches torpedos

At t = t1 + t2
target is at T2
sub is at U2
torpedo is at P2
torpedo has finished turn

At t = t1 + t2 + t3
target is at T3
sub is at U3
torpedo is at P3
torpedo impacts with target

see below






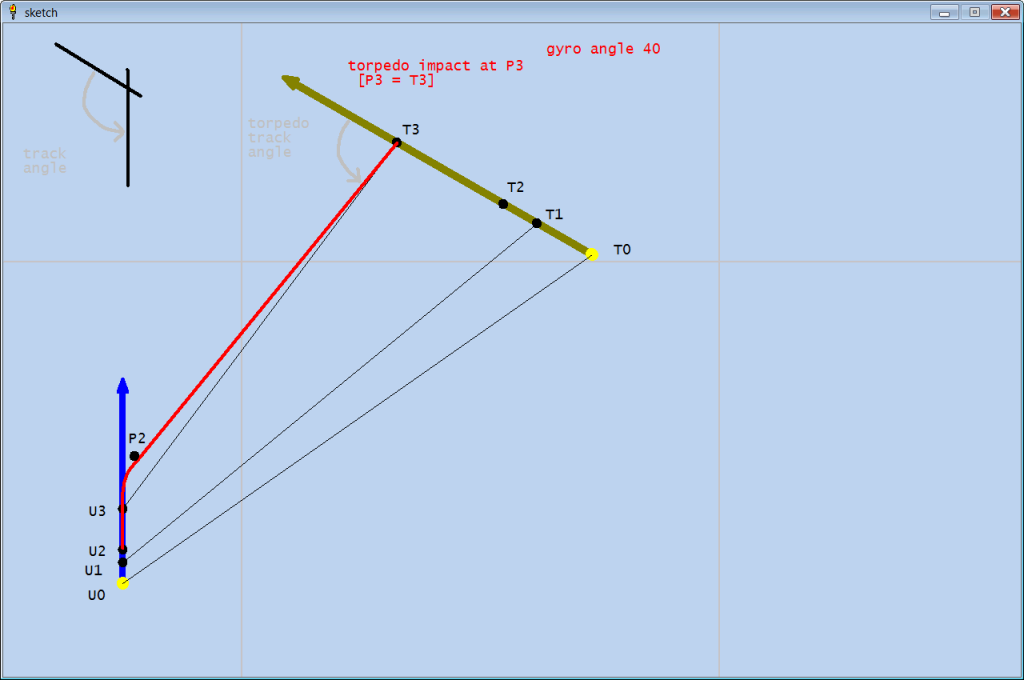
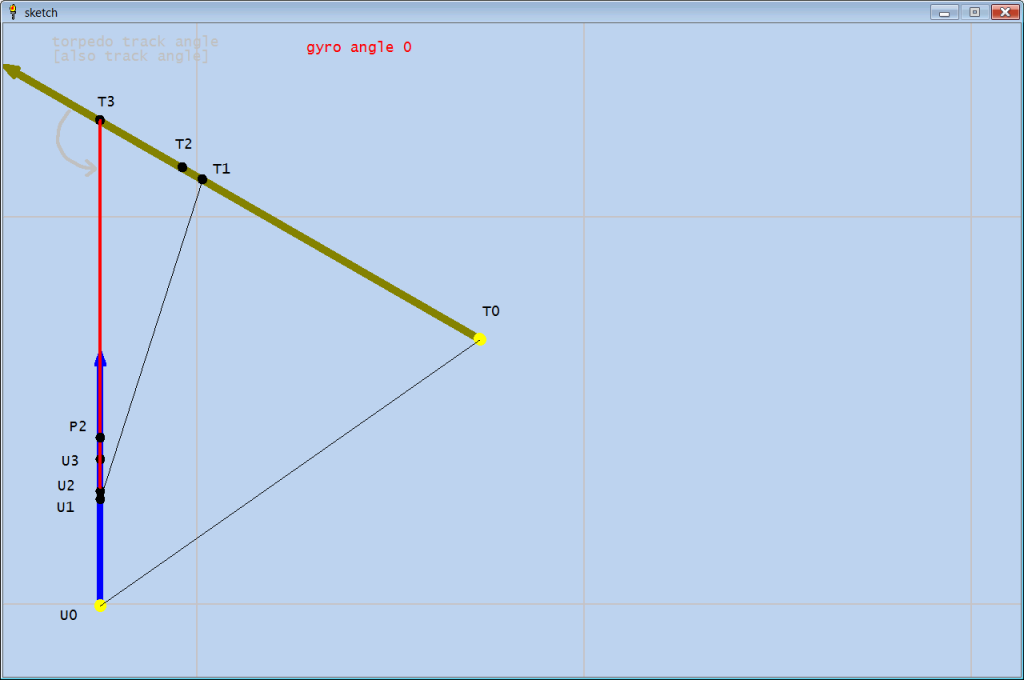
In Ex. 2, all initial sub, torp, and target data is the same except the gyro angle is 0.

start readout
Kd -10.9451942
Kx 5.19615242
Ky 17.0
Kz -103.923048
Px 158
Py 0
TT 1

t1 138.093638
t2 10
t3 41.0810475

T0x 688.291724
T0y 982.982453
T1x 1102.57264
T1y 265.426863
T2x 1132.57264
T2y 213.465339
T3x 1255.81578
T3y 0.1954525e-2
U1x 276.187275
U1y 0
U2x 296.187275
U2y 0
U3x 378.34937
U3y 0
P2x 434.187275
P2y 0
P3x 1255.80823
P3y 0

tgt bearing at launch: 17.8065083
tgt bearing at impact: 0.1276243e-3

Torp Track 941.62095

Error: 0.7802254e-2

Ath1: 5.23598776
in deg.: 300
Abg1: 0.95993109
in deg.: 55
Agyo1: 0
in deg.: 0

This shows the math works just as well for 0 gyro angle shots.




In Ex. 3, again, everything is the same except the gyro angle is -20. This gives a less favorable track, but might be necessary if you had to delay your launch for some reason.

start readout
Kd -13.8806698
Kx -1.64425044
Ky 15.7938524
Kz -77.1345132
Px 192.202014
Py -6.03073792
TT 1

t1 193.104632
t2 11.7453293
t3 45.8665896

T0x 688.291724
T0y 982.982453
T1x 1267.60562
T1y -20.4186501
T2x 1302.84161
T2y -81.4491711
T3x 1440.44138
T3y -319.778962
U1x 386.209265
U1y 0
U2x 409.699923
U2y 0
U3x 501.433102
U3y 0
P2x 578.411279
P2y -6.03073792
P3x 1440.42119
P3y -319.776689

tgt bearing at launch: 358.672909
tgt bearing at impact: 341.193741

Torp Track 1072.23838

Error: 0.20310576e-1

Ath1: 5.23598776
in deg.: 300
Abg1: 0.95993109
in deg.: 55
Agyo1: 5.93411946
in deg.: 340.0




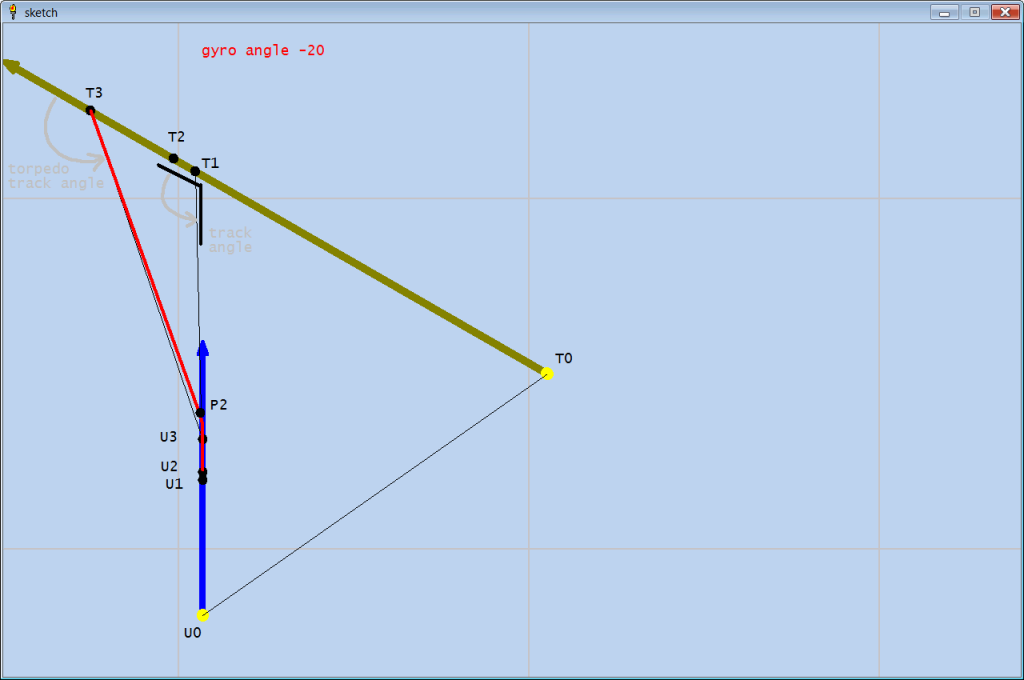
I'll post some examples which show the details of the torpedo turning better. The sketches don't really allow you to see the turning part very well, unless you are zoomed in pretty close.

TorpX