http://en.wikipedia.org/wiki/Target_Data_Computer

The TDC was designed to provide fire-control solutions for submarine
torpedo launches against
ships running on the surface (surface warships used a different computer for their torpedo launches).
[4] The TDC had a wide array of handcranks, dials and switches for data input and display.
[5] To generate a fire control solution, it required inputs on
The TDC performed the
trigonometric calculations required to compute a target intercept course for the torpedo. It also had an electromechanical interface to the torpedoes that allowed it to automatically set the torpedo courses while they were in their tubes, ready to be launched.
The TDC's target tracking capability was used by the fire control party to continuously update the fire control solution to the torpedoes even while the submarine was maneuvering. The TDC's target tracking ability also allowed the submarine to accurately launch torpedoes even when the target was temporarily obscured by smoke or fog.
TDC functional description
Since the TDC actually performed two separate functions, generating target position estimates and computing torpedo firing angles, the TDC actually consisted of two types of analog computers:
- Angle solver: This computer calculates the required gyro angle. The TDC had separate angle solvers for the forward and aft torpedo tubes.
- Position keeper: This computer generates a continuously updated estimate of the target position based on earlier target position measurements.[35]
[edit] Angle solver
The equations implemented in the angle solver can be found in the Torpedo Data Computer manual.
[36] The Submarine Torpedo Fire Control Manual
[37] discusses the calculations in a general sense and a greatly abbreviated form of that discussion is presented here.
The general torpedo fire control problem is illustrated in Figure 2. The problem is made more tractable if we assume:
- The periscope is on the line formed by the torpedo running along its course
- The target moves on a fixed course and speed
- The torpedo moves on a fixed course and speed


Figure 3: The Torpedo Fire Control Triangle
As can be seen in Figure 2, these assumptions are not true in general because of the torpedo ballistic characteristics and torpedo tube parallax. Providing the details as to how to correct the torpedo gyro angle calculation for ballistics and parallax is complicated and beyond the scope of this article. Most discussions of gyro angle determination take the simpler approach of using Figure 3, which is called the torpedo fire control triangle.
[7][8] Figure 3 provides an accurate model for computing the gyro angle when the gyro angle is small, usually less than < 30o.
[38]
The effects of parallax and ballistics are minimal for small gyro angle launches because the course deviations they cause are usually small enough to be ignorable. U.S. submarines during World War II preferred to fire their torpedoes at small gyro angles because the TDC's fire control solutions were most accurate for small angles.
[39]
The problem of computing the gyro angle setting is a trigonometry problem that is simplified by first considering the calculation of the deflection angle, which ignores torpedo ballistics and parallax.
[40] For small gyro angles,
***952;Gyro ***8776; ***952;Bearing - ***952;Deflection. A direct application of the
law of sines to Figure 3 produces Equation 1.
(Equation 1)

where
vTarget is the velocity of the target.
vTorpedo is the velocity of the torpedo.
***952;Bow is the angle of the target ship bow relative to the periscope line of sight.
***952;Deflection is the angle of the torpedo course relative to the periscope line of sight.Range plays no role in Equation 1, which is true as long as the three assumptions are met. In fact, Equation 1 is the same equation solved by the mechanical sights of
steerable torpedo tubes used on surface ships during World War I and World War II. Torpedo launches from steerable torpedo tubes meet the three stated assumptions well. However, an accurate torpedo launch from a submarine requires parallax and torpedo ballistic corrections when gyro angles are large. These corrections require knowing range accurately. When the target range was not known, torpedo launches requiring large gyro angles were not recommended.
[41]
Equation 1 is frequently modified to substitute track angle for deflection angle (track angle is defined in Figure 2,
***952;Track=***952;Bow+***952;Deflection). This modification is illustrated with Equation 2.
(Equation 2)

where
***952;Track is the angle between the target ship's course and the torpedo's course.
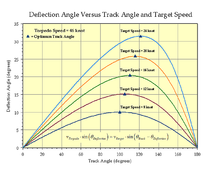

Figure 4: Deflection Angle Versus Track Angle and Target Speed (
***952;Gyro = 0o).
A number of publications
[42][43] state the optimum torpedo track angle as 110o for a Mk 14 (46 knot weapon). Figure 4 shows a plot of the deflection angle versus track angle when the gyro angle is 0o (
i.e.,
***952;Deflection=***952;Bearing).
[44] Optimum track angle is defined as the point of minimum deflection angle sensitivity to track angle errors for a given target speed. This minimum occurs at the points of zero slope on the curves in Figure 4 (these points are marked by small triangles).
The curves show the solutions of Equation 2 for deflection angle as a function of target speed and track angle. Figure 4 confirms that 110o is the optimum track angle for a 16-knot (30 km/h) target, which would be a common ship speed.
[45]
There is fairly complete documentation available for a Japanese torpedo fire control computer that goes through the
details of correcting for the ballistic and parallax factors. While the TDC may not have used exactly the same approach, it was likely very similar.
[edit] Position keeper
As with the angle solver the equations implemented in the angle solver can found in the Torpedo Data Computer manual.
[36] Similar functions were implemented in the rangekeepers for surface ship-based fire control systems. For a general discussion of the principles behind the position keeper, see
Rangekeeper.